<u id="udx2b"></u>
2021-11-04 18:44:01 公務員考試網 
 文章來源:云南分院
文章來源:云南分院
各位正在備考的小伙伴們,大家好!今天我們來學習數量關系中的三元一次方程特定題型的解題技巧。相信很多小伙伴對于賦零法解三元一次方程都有所了解,但是又比較疑惑到底什么情況下使用一定是正確的,為什么有時候賦0法就不適用,今天我們就來解決這個問題。
首先我們先來看一個例題,讓大家了解一下賦零法。
例1.(2009 國考)甲買了3支簽字筆、7支圓珠筆和1支鉛筆,共花了32元,乙買了4支同樣的簽字筆、10支圓珠筆和1支鉛筆,共花了4 3元。如果同樣的簽字筆、圓珠筆、鉛筆各買一支,共用多少錢?
A. 21元 B. 11元 C. 10元 D. 17元
解析:設簽字筆、圓珠筆和鉛筆的單價分別為x、y、z,可得兩個方程3x+7y+z=32①、4x+10y+z=43②,求x+y+z的和是多少。兩個方程三個未知項是無法直接確定x、y、z的具體數值的,提供兩種常見思路。
解法一 :湊系數法,因為我們要求的是x+y+z的整體,所以每一項的系數都應該為1,那么我們優先解決系數最復雜的一項,通過觀察后發現,兩個方程系數最復雜的項應該是x的系數,系數分別為7和10,接下來把7和10的倍數分別枚舉下來,分別為7、14、21、28、35和10、20、30、40等,觀察后發現他們的公倍數只有21減去20為1,因此我們將①×3減去②就可以將x、y、z的系數變為1,因此最后的結果為32×3-43×2=10元,選擇C選項。
解法二:賦零法,首先我們分析x、y、z里系數最復雜的未知項,顯然是x,令x=0,那么兩個方程就變成了3x+z=32、4x+z=43,兩式相減可以求得x=11,然后代入求得z=-1,所以x+y+z=11+0-1=10,選C選項。
分析兩個方法后我們發現,明顯賦零法解題更加方便簡潔。湊系數法雖看似方便,但在實際解題過程中,在將系數湊為1時往往會遇到困難,并沒有賦零法解題方便。那么小伙伴就會想,是不是所有的三元一次方程問題都可以這樣求解呢?肯定不是的,接下來我們看兩個反例。
例2.(2014 吉林)某學校組織一次教工接力比賽,共準備了25件獎品分發給獲得一、二、三等獎的職工,為設計獲得各級獎勵的人數,制定兩種方案:若一等獎每人發5件,二等獎每人發3件,三等獎每人發2件,剛好發完獎品;若一等獎每人發6件,二等獎每人發3件,三等獎每人發1件,也剛好發完獎品,則獲得二等獎的教工有多少人?
A.6 B.5 C.4 D.3
解析:設一等獎、二等獎和三等獎的教工人數分別為x、y、z人,可得兩個方程5x+3y+2z=25①、6x+3y+z=25②。我們發現此題需要求解的是y的值,那么明顯將x或z賦予不同的值,求解出來的結果是不一樣的,因此不能用賦值法。此題的正確解法應該是將不定方程組轉化為不定方程來求解。②×2-①=7x+3y=25,通過代入排除可確定y=6,因此選擇A選項。
此題不能用賦零法的原因在于求解的只是y的值,并不是x+y+z的整體。我們再來看一個例子。
例3. 某次數學競賽準備了22支鉛筆作為獎品發給一、二、三等獎的學生,原計劃一等獎每人發6支,二等獎每人3支,三等獎每人發2支。后來又改為一等獎每人發9支,二等獎每人4支,三等獎每人1支,總共有多少人獲獎?
A.5 B.6 C.7 D.8
解析:設一等獎、二等獎和三等獎的學生人數分別為x、y、z人,可得兩個方程6x+3y+2z=22①、9x+4y+z=22②。通過觀察后我們求的是整體,我們先用賦零法試一下。因為x的系數最復雜,因此令x=0,可得5y=22,y=4.4,代入解得z=4.4,此時x+y+z=8.8不是整數,但人數必須要是整數,很明顯不符合實際,因此也不能使用。看到這各位小伙伴可能會想,這也不能用,那也不能用,那學了干啥咧!各位小伙伴別著急,我們先來看這道題的正確解法,將②×2- ①=12x+5y=22,賦值代入可得唯一解x=1、y=2,代入得z=5,所以總人數=x+y+z=8,因此選擇D選項。
此題雖然求的是整體,但是由于要求x、y、z都必須是整數,所以也不能用賦零法。
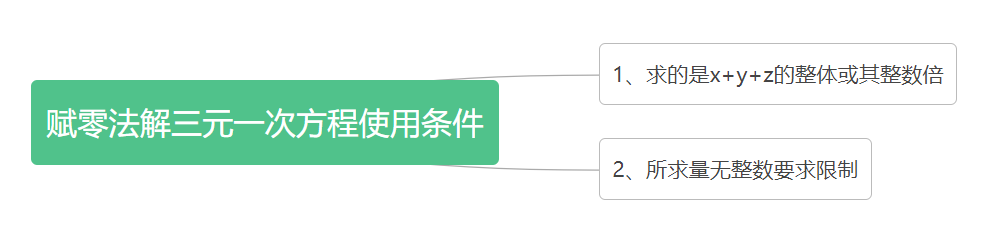
給大家總結分析一下,在解決三元一次方程時,什么情況下能使用賦值法。首先要求求的必須是整體(x+y+z的總和),其次是要求求的量沒有整數要求的限制,常見的比如金錢就不要求必須為整數,但具體人數就必須為整數。簡單分析一下原理,題目要求我們求解的是x+y+z的總和或者x+y+z的整數倍,那么x+y+z的結果必然為定值,它在實數的范圍內有無數組解,你可以嘗試令x為任意值,在實數范圍內總能找到一組y和z的值,滿足x+y+z等于定值,但是如果限制整數那就不一定能找到滿足條件的y和z的值。
接下來再把今天的知識點梳理為以下思維導圖,方便大家理解。

| ↓↓↓↓2024年國家公務員考試相關推薦↓↓↓↓ | |||
| 公考第一課 | 2024版國考圖書 | 第18版5100題 | 申論答題紙 |
| 系統提升班plus | 筆試悅享班 | 歷年臻題 | APP會員年卡 |
相關內容推薦:
2024年國家公務員考試數量關系

貼心微信客服

貼心微博客服

報名條件?
崗位選擇?
筆試科目?
面試方式?
......

 在線客服×
在線客服×國家公務員考試公告 國家公務員考試大綱 國家公務員考試專業分類目錄 國家公務員考試職位表 國家公務員考試報名入口 國家公務員考試報考條件 國家公務員考試報名費用 國家公務員考試報名人數 國家公務員考試報名確認 國家公務員考試準考證打印 國家公務員考試行測備考 國家公務員考試申論備考 國家公務員考試考試時間 國家公務員考試考試流程 國家公務員考試考試科目 國家公務員考試答題須知 國家公務員考試考場規則 國家公務員考試真題解析 國家公務員考試成績查詢 國家公務員考試分數線 國家公務員面試公告 國家公務員面試名單 國家公務員考試資格復審 國家公務員考試調劑名單 國家公務員面試技巧 國家公務員面試禮儀 國家公務員結構化面試 國家公務員無領導小組討論 國家公務員考試體檢考察 國家公務員考試錄用公示