<u id="udx2b"></u>
2021-07-09 10:43:53 公務員考試網 
 文章來源:黑龍江分院
文章來源:黑龍江分院
數量關系中有一種題型叫最值問題,它分為最不利構造、數列構造、多集合反向構造三種小題型。這種題型如果不用技巧,直接利用枚舉或其它方式做的時候很難快速解題,這里給大家分享一下最常考的兩種最值問題的題型特點以及計算方法。
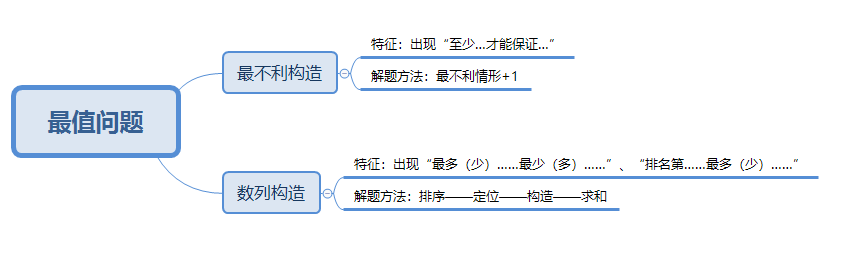
最不利構造
題型判定:題目中出現“至少…才能保證…”
解題方法:最不利情形:即保證值-1;如果部分值<保證值-1時,直接照抄計算即可
答案=“最不利情形+1”
【例1】(2020深圳)某演唱會主辦方為觀眾準備了白紅橙黃綠藍紫7種顏色的熒光棒各若干只,每名觀眾可在入口處任意選取2只,若每種顏色的熒光棒都足夠多,那么至少( )名觀眾中,一定有兩人選取的熒光棒顏色完全相同。
A.14 B.22
C.28 D.29
【解析】第一步,根據題目最后出現特征“至少…才能保證…”,確定本題考查最不利構造。
第二步,找到最不利情形是要保證值-1,即2-1=1人,那最不利的情形就是每個人選取的熒光棒都不完全相同,即若觀眾選取的是2支同色的熒光棒有=7(種)方式,若觀眾選取的是2支不同顏色的熒光棒有= 21(種)方式,共有7+21=28(種)方式。答案應為“最不利情形+1”,即至少有28+1=29(名)觀眾才能保證一定有兩人選取的熒光棒顏色完全相同。
因此,選擇D選項。
【例2】(2019重慶)某地區招聘衛生人才,共接到600份不同求職者的簡歷。其中,臨床、口腔、公共衛生和護理專業分別有200人、160人、140人和100人,問至少有多少人被錄用,才能保證一定有140名被錄用者專業相同?
A.141 B.240
C.379 D.518
【解析】第一步,根據題目最后出現特征“至少…才能保證…”,確定本題考查最不利構造。
第二步,要保證140名錄用者專業相同,則最不利的情形是只有140-1=139名滿足,則所有的最不利情形=139+139+139+100=517(名),則所求=517+1=518(名)。即至少有518人錄用,才能保證一定有140名錄用者專業相同。
因此,選擇D選項。
數列構造
題型判定:題目特征:出現“最多(少)……最少(多)……”、“排名第……最多(少)……”
解題方法:排序——定位——構造——求和
【例1】(2021廣東)某街道服務中心的80名職工通過相互投票選出6名年度優秀職工,每人都只投一票,最終A、B、C、D、E、F這6人當選。已知A票數最多,共獲得20張選票;B、C兩人的票數相同,并列第2;D、E兩人票數也相同,并列第3;F獲得10張選票,排在第4。那么B、C獲得的選票最多為( )張。
A.11 B.12
C.13 D.14
【解析】第一步,本題考查最值問題,屬于數列構造。
第二步,80人共投出80張票,若使得B、C獲得的選票最多,則A、D、E、F票數盡量少。已知A票數最多,共獲得20張選票,F獲得10張選票;因此盡量讓D、E的票數最少,且高于F,均是11票。
第三步,B、C共獲得最多票數為80-20-10-11×2=28(張),B、C兩人的票數相同,則B=C=28÷2=14(張)。
因此,選擇D選項。
【例2】(2019江西)某高校計劃招聘81名博士,擬分配到13個不同的院系,假定院系A分得的博士人數比其他院系都多,那么院系A分得的博士人數至少有多少名?
A.6B.7
C.8D.9
【解析】第一步,本題考查最值問題中的數列構造問題。
第二步,總共招聘81名博士,要想院系A分得的博士數最少,則應構造其余院系分得的博士數盡可能多。設院系A分得博士x名,那么其余12個院系最多均有x-1名,可列方程:x+(x-1)×12=81,解得x≈7.2,那么院系A分得的博士至少有8名。
因此,選擇C選項。
注意:在審題的過程中要注意區分最多和都多,還要注意是否可以有相同的情況。


| ↓↓↓↓2024年國家公務員考試相關推薦↓↓↓↓ | |||
| 公考第一課 | 2024版國考圖書 | 第18版5100題 | 申論答題紙 |
| 系統提升班plus | 筆試悅享班 | 歷年臻題 | APP會員年卡 |

貼心微信客服

貼心微博客服

報名條件?
崗位選擇?
筆試科目?
面試方式?
......

 在線客服×
在線客服×國家公務員考試公告 國家公務員考試大綱 國家公務員考試專業分類目錄 國家公務員考試職位表 國家公務員考試報名入口 國家公務員考試報考條件 國家公務員考試報名費用 國家公務員考試報名人數 國家公務員考試報名確認 國家公務員考試準考證打印 國家公務員考試行測備考 國家公務員考試申論備考 國家公務員考試考試時間 國家公務員考試考試流程 國家公務員考試考試科目 國家公務員考試答題須知 國家公務員考試考場規則 國家公務員考試真題解析 國家公務員考試成績查詢 國家公務員考試分數線 國家公務員面試公告 國家公務員面試名單 國家公務員考試資格復審 國家公務員考試調劑名單 國家公務員面試技巧 國家公務員面試禮儀 國家公務員結構化面試 國家公務員無領導小組討論 國家公務員考試體檢考察 國家公務員考試錄用公示